素数的判断算法比较
|
465
|
基础算法

793 字
|
22 分钟

素数的判断算法比较

参与对比的几个素数判断算法：

朴素算法 朴素算法的平方优化 Miller-Rabin 素性测试 埃筛 线性筛
判断单个素数的时间复杂度 $O(n)$ $O(\sqrt{n})$ $O(k;log^3;n)$ ($k$为进行$k$轮检测) $O(n;log;log;n)$ $O(n)$

对于朴素算法以及素性测试，判断单个素数用时较短，且受输入数据范围影响较大，这里进行多次运算求累计时间；
对于素数筛法，通常按照数据范围的最大值进行处理，这里采用固定的 $100000000$（$1e8$）进行预处理。

对比结果

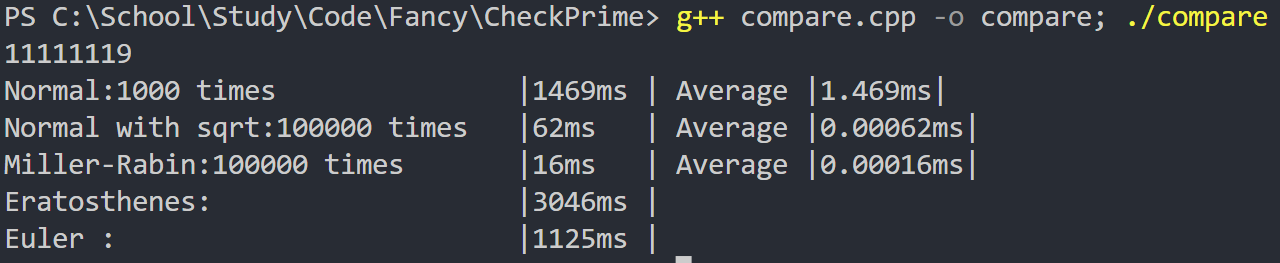
compare-result

根据分析结果进行简单计算：
$$
3046 \div 0.0016 = 19037500
$$

因此可以猜测，对于范围相近的数据，如果检查的次数在 $2e7$ 次左右，则使用 Miller-Rabin 算法与使用 Eratosthenes（埃筛）筛法所需时间大致相同；

compare-result

但是 Miller-Rabin 算法的时间与待检测的数字有关，不同的数据范围会有不同的运算时间：

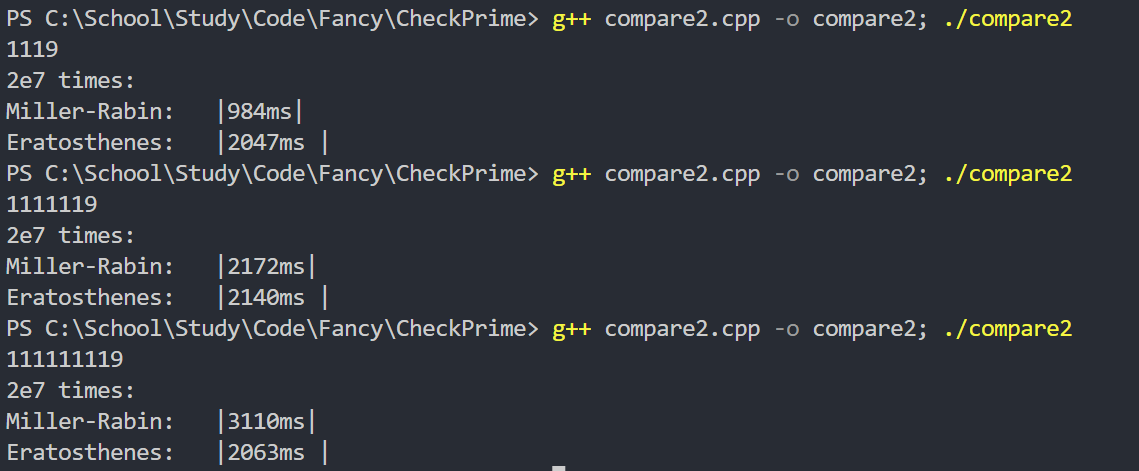
compare-result

如果我们将范围限定在$[1e8,1e8+2e7)$之间，结果如下：

compare-result

对于筛法，虽然在某些场景下性能类似甚至更为高效，但是其空间开销较大，同时对于较大的数字无法进行判断，仍存在一些缺陷。

对比程序

compare1

#include <iostream>
#include <windows.h>
using namespace std;

const long long N = 1e8;

bool isPrime1[N];
int isPrime2[N];
int num[N];

long long qpow(long long a, long long b, long long m)
{
    long long res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % m;
        a = a * a % m;
        b >>= 1;
    }
    return res % m;
} // O(log a);

bool Miller_Rabin(long long x, long long n)
{
    long long b = n - 1;
    while (!(b & 1))
        b >>= 1;
    x = qpow(x, b, n);
    while (b < n - 1 && x != 1 && x != n - 1)
        x = (x * x) % n, b <<= 1;
    return x == n - 1 || b & 1 == 1;
}

bool check_prime1(long long n)
{
    bool flag = 1;
    for (int i = 2; i < n; i++)
    {
        if (n % i == 0)
        {
            flag = 0;
            break;
        }
    }
    return flag;
}

bool check_prime2(long long n)
{
    bool flag = 1;
    for (int i = 2; i * i < n; i++)
    {
        if (n % i == 0)
        {
            flag = 0;
            break;
        }
    }
    return flag;
}

bool check_prime3(long long n)
{
    if (n == 2 || n == 7 || n == 61)
        return true;
    if (n == 1 || !(n & 1))
        return false;
    return Miller_Rabin(2, n) && Miller_Rabin(7, n) && Miller_Rabin(61, n);
}

void check_prime4()
{
    for (int i = 2; i <= N; i++)
    {
        if (isPrime1[i] == 0)
        {
            for (int j = 2; j * i < N; j++)
            {
                isPrime1[i] = 1;
            }
        }
        else
        {
            continue;
        }
    }
}

int check_prime5()
{
    int index;
    for (int i = 2; i < N; i++)
    {
        // 如果未标记则得到一个素数
        if (num[i] == 0)
            isPrime2[++index] = i;
        // 标记目前得到的素数的i倍为非素数
        for (int j = 1; j <= index && isPrime2[j] * i < N; j++)
        {
            num[i * isPrime2[j]] = 1;
            if (i % isPrime2[j] == 0)
                break;
        }
    }
    return index;
}

int main()
{
    long long n;
    cin >> n;
    int start, end;

    // 朴素算法
    cout << "Normal:1000 times\t\t|";
    start = GetTickCount();
    for (int i = 0; i < 1000; i++)
    {
        check_prime1(n);
        n++;
    }
    end = GetTickCount() - start;
    cout << end << "ms\t|";
    cout << " Average |"
         << (double)(end / 1000.0) << "ms|\n";

    // 朴素算法的平方优化
    cout << "Normal with sqrt:100000 times\t|";
    start = GetTickCount();
    for (int i = 0; i < 100000; i++)
    {
        check_prime2(n);
        n++;
    }
    end = GetTickCount() - start;
    cout << end << "ms\t|";
    cout << " Average |"
         << (double)(end / 100000.0) << "ms|\n";

    // Miller-Rabin  素性测试
    cout << "Miller-Rabin:100000 times\t|";
    start = GetTickCount();
    for (int i = 0; i < 100000; i++)
    {
        check_prime3(n);
    }
    end = GetTickCount() - start;
    cout << end << "ms\t|";
    cout << " Average |"
         << (double)(end / 100000.0) << "ms|\n";

    // 埃筛
    cout << "Eratosthenes:\t\t\t|";
    start = GetTickCount();
    check_prime4();
    end = GetTickCount() - start;
    cout << end << "ms\t|" << endl;

    // 线性筛
    cout << "Euler :\t\t\t\t|";
    start = GetTickCount();
    check_prime5();
    end = GetTickCount() - start;
    cout << end << "ms\t|" << endl;
    // system("pause");
    return 0;
}

compare2

#include <iostream>
#include <windows.h>
using namespace std;

const long long N = 1e8;

bool isPrime1[N];
int isPrime2[N];
int num[N];

long long qpow(long long a, long long b, long long m)
{
    long long res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % m;
        a = a * a % m;
        b >>= 1;
    }
    return res % m;
} // O(log a);

bool Miller_Rabin(long long x, long long n)
{
    long long b = n - 1;
    while (!(b & 1))
        b >>= 1;
    x = qpow(x, b, n);
    while (b < n - 1 && x != 1 && x != n - 1)
        x = (x * x) % n, b <<= 1;
    return x == n - 1 || b & 1 == 1;
}

bool check_prime3(long long n)
{
    if (n == 2 || n == 7 || n == 61)
        return true;
    if (n == 1 || !(n & 1))
        return false;
    return Miller_Rabin(2, n) && Miller_Rabin(7, n) && Miller_Rabin(61, n);
}

void check_prime4()
{
    for (int i = 2; i <= N; i++)
    {
        if (isPrime1[i] == 0)
        {
            for (int j = 2; j * i < N; j++)
            {
                isPrime1[i] = 1;
            }
        }
        else
        {
            continue;
        }
    }
}

int check_prime5()
{
    int index;
    for (int i = 2; i < N; i++)
    {
        // 如果未标记则得到一个素数
        if (num[i] == 0)
            isPrime2[++index] = i;
        // 标记目前得到的素数的i倍为非素数
        for (int j = 1; j <= index && isPrime2[j] * i < N; j++)
        {
            num[i * isPrime2[j]] = 1;
            if (i % isPrime2[j] == 0)
                break;
        }
    }
    return index;
}

int main()
{
    long long n;
    cin >> n;
    int start, end;

    cout << "2e7 times:\n";
    // Miller-Rabin  素性测试
    cout << "Miller-Rabin:\t|";
    start = GetTickCount();
    for (int i = 0; i < 20000000; i++)
    {
        check_prime3(n);
    }
    end = GetTickCount() - start;
    cout << end << "ms|\n";

    // 埃筛
    cout << "Eratosthenes:\t|";
    start = GetTickCount();
    check_prime4();
    for (int i = 10; i < 20000010; i++)
    {
        if (isPrime1[i])
        {
            ;
        }
        else
        {
            ;
        }
    }
    end = GetTickCount() - start;
    cout << end << "ms\t|" << endl;
    return 0;
}

compare3

#include <iostream>
#include <windows.h>
using namespace std;

const long long N = 1e8;

bool isPrime1[N];
int isPrime2[N];
int num[N];

long long qpow(long long a, long long b, long long m)
{
    long long res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % m;
        a = a * a % m;
        b >>= 1;
    }
    return res % m;
} // O(log a);

bool Miller_Rabin(long long x, long long n)
{
    long long b = n - 1;
    while (!(b & 1))
        b >>= 1;
    x = qpow(x, b, n);
    while (b < n - 1 && x != 1 && x != n - 1)
        x = (x * x) % n, b <<= 1;
    return x == n - 1 || b & 1 == 1;
}

bool check_prime3(long long n)
{
    if (n == 2 || n == 7 || n == 61)
        return true;
    if (n == 1 || !(n & 1))
        return false;
    return Miller_Rabin(2, n) && Miller_Rabin(7, n) && Miller_Rabin(61, n);
}

void check_prime4()
{
    for (int i = 2; i <= N; i++)
    {
        if (isPrime1[i] == 0)
        {
            for (int j = 2; j * i < N; j++)
            {
                isPrime1[i] = 1;
            }
        }
        else
        {
            continue;
        }
    }
}

int check_prime5()
{
    int index;
    for (int i = 2; i < N; i++)
    {
        // 如果未标记则得到一个素数
        if (num[i] == 0)
            isPrime2[++index] = i;
        // 标记目前得到的素数的i倍为非素数
        for (int j = 1; j <= index && isPrime2[j] * i < N; j++)
        {
            num[i * isPrime2[j]] = 1;
            if (i % isPrime2[j] == 0)
                break;
        }
    }
    return index;
}

int main()
{
    long long n;
    // cin >> n;
    int start, end;

    cout << "2e7 times:\n";
    // Miller-Rabin  素性测试
    cout << "Miller-Rabin:\t|";
    start = GetTickCount();
    for (int i = 0; i < 20000000; i++)
    {
        check_prime3(i + 100000000);
    }
    end = GetTickCount() - start;
    cout << end << "ms|\n";

    // 埃筛
    cout << "Eratosthenes:\t|";
    start = GetTickCount();
    check_prime4();
    for (int i = 10; i < 20000010; i++)
    {
        if (isPrime1[i])
        {
            ;
        }
        else
        {
            ;
        }
    }
    end = GetTickCount() - start;
    cout << end << "ms\t|" << endl;
    return 0;
}
C++
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																					

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
最大公因数和最小公倍数 GCD & LCM

							
							

							
进制转换