基础概念
- 结点:数据结构的基本组成单位
- 树:n个点的有限集合,n=0的树为空树,在任意非空树中:
a. 有且仅有一个根节点
b. n>1时其他节点可以分为m个互不相交的集合,其中每个集合本身有时一棵树,同时为根的子树,如果集合发生相交,则形成一张图。 - 度:图中有入度和出度,在树中,度数为指向子节点的数量
- 结点关系:
a. 父节点(双亲节点):当前结点向上指向的结点,仅有一个
b. 子节点(孩子结点):当前结点向下指向的结点,有多个
c. 兄弟节点:具有同一个父节点 - 叶子结点:无子节点的结点
- 树的深度(节点层次):如图所示,最大的层次即为树的深度
二叉树
在上述定义的基础上,一个根节点做多仅有两个子节点的树,称为二叉树
二叉树有左子树和右子树,二者顺序不能颠倒
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
二叉树的特点:
每个节点最多有两颗子树
左右子树是由顺序的(不同的遍历方式会得到不同的结果)
即是包含空节点,也要明确顺序
二叉树的性质:
- 第i层上最多有2^(i-1)个结点
- 深度为k的二叉树最多有(2^k)-1个结点
- n0=n2+1 n0表示度数为0的节点数,n2表示度数为2的节点数
- 在完全二叉树中,具有n个节点的完全二叉树的深度为[log2n]+1,其中[log2n]是向下取整。
- 若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号,则对完全二叉树中任意一个编号为 i 的结点有如下特性
(1) 若 i=1,则该结点是二叉树的根,无双亲, 否则,编号为 [i/2] 的结点为其双亲结点;
(2) 若 2*i>n,则该结点无左孩子, 否则,编号为 2*i 的结点为其左孩子结点;
(3) 若 2*i+1>n,则该结点无右孩子结点, 否则,编号为 2*i+1 的结点为其右孩子结点。
特殊的树:
斜树,只有左子树(左斜树)或者只有右子树(右斜树)的二叉树
满二叉树,叶子结点均在同一层上,并且其余结点均具有左右节点,因此相同深度的二叉树,满二叉树结点最多,叶子最多
完全二叉树,满二叉树的叶子结点从右向左删除,即形成完全二叉树,满足以下几点
叶子结点仅出现在最下层和次下层,且最下层叶子结点在左边,次下层叶子结点在右边
叶子结点在每一层一定连续
如果节点度数为1则只有左子树没有右子树
同样节点数量的二叉树,完全二叉树深度最小
满二叉树一定是完全二叉树,反之不然
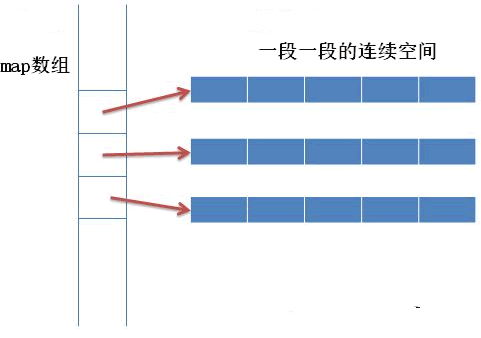
存储方式
顺序存储(指针模拟)
利用数组下标模拟树的节点坐标;
根据二叉树的性质,假定一个节点下标为i,则其父亲节点为i/2,其左节点为i*2,右节点为i*2+1;
但也正因如此,只有当树为完全二叉树的时候才能填数组,其他情况会有数组中存放空节点。
该种存储方式主要用在堆中。
二叉链表
通过链式存储,通过一个数据域两个或三个(包含父指针)指针域构成一个节点,过程类似链表的插入。
结点的定义:
struct node{
int data;
node *l,*r;
node *h;//指向父结点
}
使用数组模拟的方式较为简单再次就不赘述了,主要以链式存储为进行介绍。
二叉树的遍历:
前序遍历
中序遍历
后序遍历
层序遍历
所谓前中后序实际上就遍历到父节点的顺序,前序为父-左-右,中序为左-父-右,后序为左-右-父。
这三种不同的遍历序列,可以建出相同的树。给定中序遍历序列,另外再给出前序或后序遍历的序列即可确定一颗二叉树。
层序遍历即是按照一层一层的顺序进行,就是对树进行了一次BFS
二叉树的建立:
这里使用“,”表示空节点。
struct node{
int data;
node *l,*r;
}
node* buildtree(node *root)
{
if(a[cnt]!=',')
{
root=new node;
root->data=a[cnt++];
root->l=bulidtree(root->l);
root->r=bulidtree(root->r);//前序遍历序列生成的树。
}else {
root=NULL;
cnt++;
}
return root;
}
如果想根据其他遍历序列建树可以:
中序遍历
node* buildtree(node *root)
{
if(a[cnt]!=',')
{
root=new node;
root->l=bulidtree(root->l);
root->data=a[cnt++];
root->r=bulidtree(root->r);
}else {
root=NULL;
cnt++;
}
return root;
}
后序遍历
node* buildtree(node *root)
{
if(a[cnt]!=',')
{
root=new node;
root->l=bulidtree(root->l);
root->r=bulidtree(root->r);
root->data=a[cnt++];
}else {
root=NULL;
cnt++;
}
return root;
}
树的遍历的实现:
前中后序
如果已经建好了一棵树,想要得到他的三种序列,可以:
void preorder(node root)
{
if(root)
{
cout<<data; preorder(root->l);
preorder(root->r);
}
}
void midorder(node root)
{
if(root)
{
midorder(root->l);
cout<data; midorder(root->r);
}
}
void postorder(node root)
{
if(root)
{
cout<data; postorder(root->l);
postorder(root->r);
}
}
层序遍历:
一般是一个简单的BFS,需要借助到队列;
struct node{
int data;
node *l,*r;
}
queue <node*> q;
q.push(&root);
while(!q.empty())
{
node *t;
t=q.front();
cout<data; q.pop() if(t->l)
q.push(t->l);
if(t->r)
q.push(t->r);
}
根据不同遍历序列生成一棵树
根据前序或后序序列找到根节点;
找到根节点后,在中序序列找到该节点;
通过中序序列重新在对左右子树进行上述操作(递归)
结束条件是定位出的根节点是当前序列中的唯一一个
先序和中序
string pre,mid;
struct node
{
char data;
node *l,*r;
};
node* build(int f,int l,int r,node* root)
{
int i=l;
while(pre[f]!=mid[i])
{
i++;
}
root=new node;
root->data=mid[i];
if(l<=i-1)
{
root->l=build(f+1,l,i-1,root->l);
}else root->l=NULL;
if(i+1<=r)
{
root->r=build(f+i-l+1,i+1,r,root->r);
}else root->r=NULL;
return root;
}
后序和中序
后序和先序类似,区别在与递归时后序序列中根节点的下标值,
node* build(int f,int l,int r)
{
int i=l;
while(post[f]!=mid[i])
{
i++;
}
node *root=new node;
root->data=mid[i];
if(l<=i-1)
{
root->l=build(f-(r-i+1),l,i-1);
}else root->l=NULL;
if(i+1<=r)
{
root->r=build(f-1,i+1,r);
}else root->r=NULL;
return root;
}