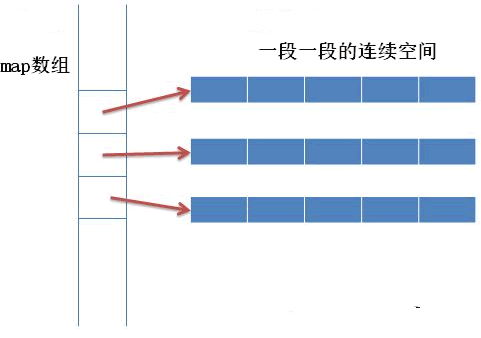
常用的 最短路 算法有三种:Floyd、Dijkstra、Bellman-Ford(SPFA),三种各有优劣。
Floyd
该算法可以计算任意两点之间的最短路径(全源最短路),算法实现简单,只需要三个for循环,但是时间复杂度高,适合数据量小的稠密图。
同时该算法可以计算负权图(不能有负环)。
该算法实现的本质是动态转移.我们使用邻接矩阵来存储更容易实现该算法。
算法原理
定义一个数组f[k][x][y]表示只经过1-K个点能取得的从x到y的最短路长度。
初始化
我们初始化这个数组的f[0][x][y]。
对于每个f[0][x][y],有三个可能的取值:
- 0。当x=y时取0.
- w。当x、y之间有直接的边相连时,边权为w,f数组取w。
- INF 当不符合以上两种条件时,f数组取INF
转移方程
在此的基础上我们可以找到动态转移方程为:
f[k][x][y]=min(f[k-1][x][y],f[k-1][x][k]+f[k-1][k][y])
f[k-1][x][y]表示不经过k点时x,y之间的最短路。
f[k-1][x][k]+f[k-1][k][y]表示x和y到k点的距离,两者之和即为经过k点从x到y的距离。
我们通过两个for循环可以遍历到任意两点[x][y] & [y][x],同时可以通过一个for循环控制从1到k,这样通过三个for循环就可以实现该算法,算法时间复杂度为O(n^3)。
优化
第一维对于结果是没有影响的,因此我们可以省略第一维来优化空间复杂度(注意,最外层循环仍然存在),具体证明暂时略,可以参考最短路 – OIWiki。
算法实现
以 SDUT – 图结构练习——最短路径 为例:
#include <bits/stdc++.h>
using namespace std;
long long f[210][210]={0};
int main()
{
int n,m;
while(cin>>n>>m)
{
for(int i=0;i<=n;i++)
{
for(int j=0;j<=n;j++)
{
f[i][j]=0x3f3f3f3f;
}
f[i][i]=0;
}
int x,y,c;
for(int i=0;i<m;i++)
{
cin>>x>>y>>c;
if(f[x][y]>c)
{
f[x][y]=c;
f[y][x]=c;
}
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
cout<<f[1][n]<<endl;
}
return 0;
}
本段代码中两个结点之间存在多条边,同时是无向图,因此在输入的时候需要存入最小边。
Dijkstra
Dijkstra算法是计算单源最短路的一种算法(起点唯一,终点不定),它适用于非负权图。
算法原理
Dijkstra算法的思想是把遍历过和没遍历过的结点分别放在S和T两个集合中。每次从T选择一个结点加入到S,然后对该节点的每一个边进行松弛操作,直到T集合为空。
松弛操作
松弛操作的原理和Floyd中的转移方程类似,我们可以把Floyd的转移方程写成下列形式:
if(f[i][j]>f[i][k]+f[k][j])
f[i][j]=f[i][k]+f[k][j];
这其实就是我们需要的松弛操作:通过一个辅助点缩小两点之间的距离,我们在Dijkstra算法中通常写成下列形式:
if(dis[v]>dis[u]+w)
dis[v]=dis[u]+w;
在这里的辅助点是u点,w是u到v的边权。
朴素算法
通过n次循环不断寻找最短的且没有加入集合T的结点,时间复杂度为O(n^2)。
for(int i=1;i<=n;i++)
{
int u=0,mdis=0x3f3f3f3f;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&dis[j]<mdis)
{
mdis=dis[j];
u=j;
}
}
vis[u]=1;
for(int j=head[u];j;j=e[j].next)
{
int v=e[j].v;
int w=e[j].w;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
}
}
}
优化
Dijkstra有多种优化,我们常用的是优先队列优化。
使用优先队列优化的原理是每次选择路径最短的结点更新,因此我们需要使用优先队列记录结点编号u以及当前路径长度dis,同时使用dis作为key由小到大排序,为了方便我们使用一个结构体存储并重载运算符:
struct node{
int dis;
int u;
bool operator > (const node &o)const{
return dis>o.dis;
}
};
priority_queue<node,vector<node>,greater<node>> q;
算法实现
这里同样以 SDUT – 图结构练习——最短路径 为例:
朴素算法
#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
struct edge
{
int next;
int v;
int w;
}e[400200];
int head[110];
int dis[110];
int vis[110]={0};
int tot=0;
int n,m;
void add_edge(int u,int v,int w)
{
e[++tot].next=head[u];
head[u]=tot;
e[tot].v=v;
e[tot].w=w;
}
void find_ans()
{
dis[1]=0;
for(int i=1;i<=n;i++)
{
int u=0,mdis=0x3f3f3f3f;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&dis[j]<mdis)
{
mdis=dis[j];
u=j;
}
}
vis[u]=1;
for(int j=head[u];j;j=e[j].next)
{
int v=e[j].v;
int w=e[j].w;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
}
}
}
}
int main()
{
while(cin>>n>>m)
{
for(int i=0;i<=n;i++)
{
dis[i]=INF;
}
memset(vis,0,sizeof vis);
memset(head,0,sizeof head);
tot=0;
int u,v,w;
for(int i=0;i<m;i++)
{
cin>>u>>v>>w;
add_edge(u,v,w);
add_edge(v,u,w);
}
find_ans();
cout<<dis[n]<<endl;
}
return 0;
}
优先队列优化
#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
struct edge
{
int next;
int v;
int w;
}e[400200];
struct node{
int dis;
int u;
bool operator > (const node &o)const{
return dis>o.dis;
}
};
int head[110];
int dis[110];
int vis[110]={0};
int tot=0;
void add_edge(int u,int v,int w)
{
e[++tot].next=head[u];
head[u]=tot;
e[tot].v=v;
e[tot].w=w;
}
void find_ans()
{
priority_queue<node,vector<node>,greater<node>> q;
q.push({0,1});
dis[1]=0;
while(q.size())
{
int u=q.top().u;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].v;
int w=e[i].w;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
q.push({dis[v],v});
}
}
}
}
int main()
{
int n,m;
while(cin>>n>>m)
{
for(int i=0;i<=n;i++)
{
dis[i]=INF;
}
memset(vis,0,sizeof vis);
memset(head,0,sizeof head);
tot=0;
int u,v,w;
for(int i=0;i<m;i++)
{
cin>>u>>v>>w;
add_edge(u,v,w);
add_edge(v,u,w);
}
find_ans();
cout<<dis[n]<<endl;
}
return 0;
}
Bellman-Ford
该算法简称BF算法,为单源最短路算法,同样使用到了松弛操作,可以计算负权图,并且可以对最短路不存在的情况作出判断。
算法原理
朴素算法
和前两种算法不同的一点是该算法是对边进行松弛,可以证明通过N-1次操作就可以找到最短路。该算法的时间复杂度是O(nm)。
SPFA 队列优化
我们通过简单的分析可以发现,很多时候算法在做无用的松弛操作。我们可以通过一个队列进行优化,当且仅当松弛操作发生时才将其连接的结点加入到队列中参与下一次松弛。
通常情况下SPFA跑的很快,但是也很容易被数据卡回O(nm)的时间复杂度。
判断负环
该算法一个特殊的地方在于他可以判断图中是否包含负环。
在朴素算法中我们在进行过N-1次操作后只需要再进行一次操作,如果仍然可以被松弛则说明图上存在负环。