图
图由顶点和边组成,有以下几种类型:
- 有向图
- 无向图
- 连通图
- 非连通图
- 完全图 //边数可计算,为1/2(n*(n-1))
图的存储
可以通过数组和vector存储,也可以通过“链式前向星”进行存储
邻接矩阵
实际上是一个二维数组,数组下表代表哪两个结点,数组的值代表是否连通或者是边权大小。
bool d[10][10]={0};
d[1][2]=1;
表示1和2之间有一条边
int d[10][10]={0};
d[1][2]=4;
表示1和2之间有一条边权为4的边
一般来说没有自环,即没有d[1][1]=1这种情况。
同时对于大数据是无法进行存储的只能使用邻接表来储存。
边缘列表
使用结构体存储所有的边,很少使用
struct edge{
int u,v
};
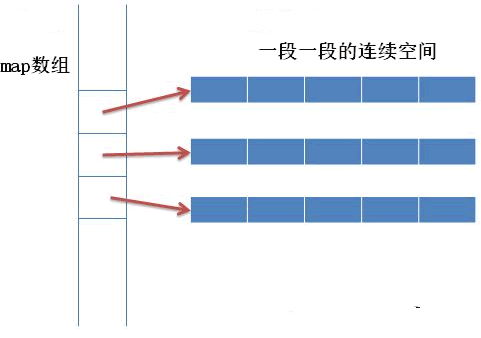
邻接表
对于一个结点,使用某种数据结构将他的所有边存储起来,将所有结点的边的信息放到一个表中,就是邻接表。
可以使用链表进行存储,但由于链表的写法有些复杂,也加容易出现问题,所以一般使用STL中的vector数组或链式前向星进行存储
vector 向量
STL中的变长数组,可以直接用数组下表访问,也可以调用STL的方法。
声明时声明为一个一维数组的vector,这样在实际上可以实现一个二维数组,由于二维的可变长特点,可以优化空间开销。
vector a[N];
vector遍历
可以使用c++的特性,利用int i:a进行遍历操作
vector <int> a;
for(int i:a)
{
cout<<i<<'\n';
}
链式前向星
使用数组下标模拟链表进行储存,可以储存边的信息,也可以储存其他的一些信息
结构体的声明
int node[N];
struct edge
{
int next; // 链表下一个元素(下一条边)的(边的)编号
int node; // 边的终点
int w; // 边的边权
}e[M];
结构体中,next表示下一条边的编号,也就是结构体数组的下标。node表示下一个结点下标,w作为可选变量表示边的权重。
加边操作
加边的时候实际上是类似链表的头插法,需要先将新节点指向当前head指向的结点,然后再让head指向新节点,完成头插。
int head[N];//储存结点的第一条边的编号
int tot=0;//
void add(int u,int v,int w)
{
e[++tot].next=head[u];
head[u]=tot;
e[tot].w=w;
e[tot].node=v;
}
遍历操作
和链表的遍历类似,如果最后一个指向的不为空,则继续遍历;
注意,一开始head数组要进行初始化,否则无法判断出来是否到达了最后
bool vis[N]={0};
void dfs(int u)
{
vis[u]=ture;
for(int i=head[u];v=e[i].node,i;i=e[i].next)//逗号表达式去最后一个表达式的值
{
if(!vis[i])
{
dfs(v);
}
}
}
图的遍历
对于临界矩阵来说可以直接根据数组进行判断结点标号;但是使用邻接表的存储方式则只能记录边。
如果想要执行kruskal算法(需要按照边权遍历所有的边),就要采用齐前向星,我们只需要一个for循环就可以解决。但如果是要遍历某一个结点的所有边,前向星可以这样做
for(int i=head[u];i;i=e[i].next)
对于vector来说可以用迭代器的方式,也可以一直pop,如果要放回的话再找一个“接住”就可以。