题目链接:全排列问题
问题分析
以 1,2,3 为例,自然思维我们会思考以 1 打头然后再去罗列之后的数字,然后以 2 打头、以 3 打头……
最终会得到如下序列:
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
我们将自然思维的过程归纳为下面一段表达:
要确定N个数的全排列,首先固定一个数,然后考虑剩下N-1个数的全排列。
在上述表达中可以发现原来的问题被分解成了一个类似子问题,对于这种问题,我们可以使用递归的方式进行求解。
递归过程
根据前文中的表达,我们可以将递归函数的内容划分为如下两个步骤:
- 选择好确定的数字
- 确定好递归的状态,进行下一层递归
以一个 3 位数的全排列为例,在最终结果中,每一位都有 $C\binom {1} {3}$ 种可能性,即 1 2 3 均遍历一遍。
对于更多的,如 N 位时则会有 $C\binom {1} {N}$ 种情况,即 1 到 N 均遍历一遍。
因为每一位都要经历 1 到 N 的遍历,因此这个过程可以使用 for 循环来实现。
代码实现
对于一个 N 位数的全排列,其每一位的选择如下:
$C\binom {1} {N} C\binom {1} {N-1} C\binom {1} {N-2} \ldots C\binom {1} {2} C\binom {1} {1}$
可以观察到每一位的选择是逐渐减少的,这是因为数字不能重复选择。
下段代码中使用了变量 f 来标记是否已经选择过,在 for 循环中会对其进行判断,避免重复选择。
#include<stdio.h>
#include<stdlib.h>
struct number{
int num;
int f;
}a[20];//结构体数组
void out(int ans[],int n)//格式化输出
{
for(int i=0;i<n;i++)
{
if(i!=n-1)printf("%d,",ans[i]);
else printf("%d\n",ans[i]);
}
}
void solve(struct number a[],int ans[],int n,int tail)
{
if(tail==n) out(ans,n);
for(int i=0;i<n;i++)
{
if(!a[i].f)
{
a[i].f=1;
ans[tail]=a[i].num;
solve(a,ans,n,tail+1);
a[i].f=0;
}
}
}
int main()
{
int n;
int ans[20];
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d", &a[i].num);
}
find(a,ans,n,0);
return 0;
}
其他方法?
在上面我们使用额外的 f 以及 ans 数组进行辅助求解,但我们可以重新分析一下这个过程:
重新分析
在上述方法中使用了 f 对数字进行了标记,目的是判断该数字是否被选择过。
我们进一步抽象,将被 f 标记过的数字放入一个集合 $S1$ ;将其他数字放入候选集合 $S2$ ,集合 $S1$ $S2$ 互为补集。当 $|S2|$ 为 0 时即为边界条件,可以输出答案。
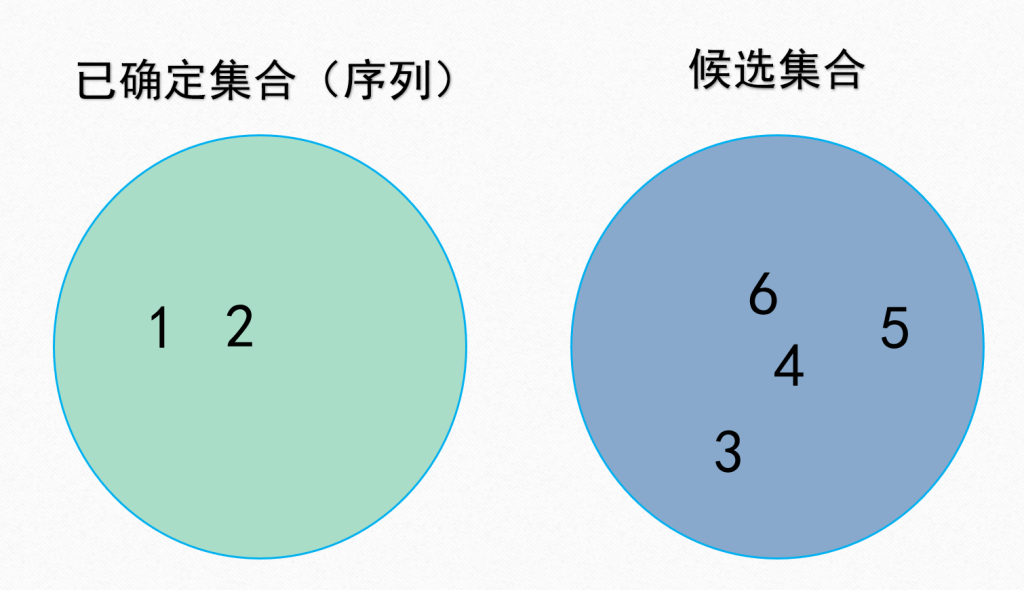
集合 S1 和 集合 S2
通过互为补集的性质,我们可以尝试在一个数组上实现问题的求解。
一个 a 数组
使用一个指针 K 将数组划分为两个部分,其中左边为已确定的序列、右边为候选序列(集合),对于指针 k 指向的位置,即为我们当前需要确定数字的位置。
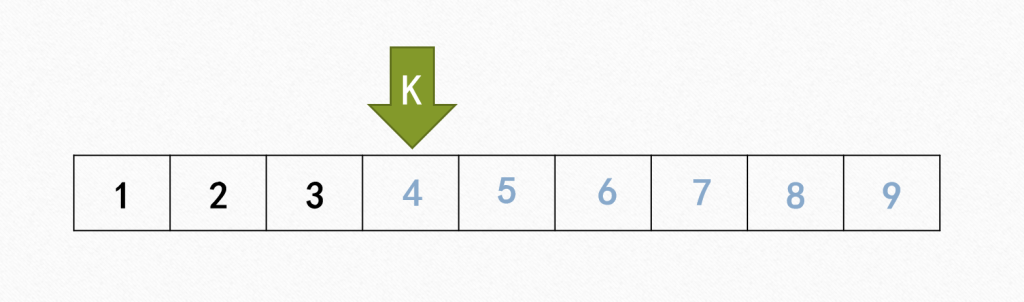
黑色为确定部分,淡蓝色为候选部分
指针 k 可以选择的数字在它(包括它)右边的候选序列中,此时若要遍历候选序列,就要遍历 $ ak \ldots aN-1$ ,在遍历时我们只需要将数字与 $ak$ 交换,递归传递 k+1 进入下一层即可实现确定第 k 个数字。
当函数回溯后只需交换复原候选序列,然后进入下一次循环继续确定 $ak$ 直至 k=N-1 结束。
代码实现
#include<stdio.h>
#include<stdlib.h>
void out(int a[],int n)
{
for(int i=0;i<n;i++)
{
if(i!=n-1)printf("%d,",a[i]);
else printf("%d\n",a[i]);
}
}
void swap(int *a,int *b)
{
int t=*a;
*a=*b;
*b=t;
}
void solve(int a[],int k,int m)
{
if(k==m) out(a,m+1);
for(int i=k;i<=m;i++)//代码核心
{
swap(&a[k],&a[i]);
solve(a,k+1,m);
swap(&a[k],&a[i]);
}
}
int main()
{
int n;
scanf("%d", &n);
int a[20];
for(int i=0;i<n;i++)
{
scanf("%d", &a[i]);
}
solve(a,0,n-1);
return 0;
}
等等,好像有点不对劲
没错,上述程序确实找出了所有的全排列,但是它输出的顺序并不满足文首链接中的题目要求。
| First | Second |
|---|---|
| 1,2,3 | 1,2,3 |
| 1,3,2 | 1,3,2 |
| 2,1,3 | 2,1,3 |
| 2,3,1 | 2,3,1 |
| 3,2,1 | 3,1,2 |
| 3,1,2 | 3,2,1 |
问题就在最后两个,上述代码中并非按照题目要求的顺序输出。这是什么原因呢?
我们借助一个更长的例子来解释:
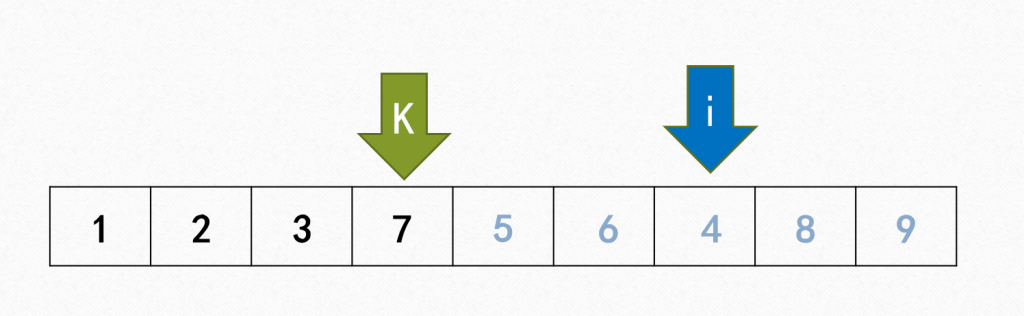
注意,顺序乱了!
当 k 与 i 交换后确定了当前 $ak$ 为 7 ,但候选序列产生了一段非递增序列,如果我们不去维护,在上述状态下我们会首先得到序列:$ 1,2,3,7,5,6,4,8,9 $ 并非我们所期望的 $ 1,2,3,7,4,5,6,8,9 $ ,在此基础上继续递归得到的顺序依旧是乱序的。
想要解决这个问题就要将这一段非递增序列变为递增序列,解决方法很简单,只需要在交换之后将数组右移,并把最右侧元素向左移动最左侧即可,当函数回溯时再进行一次逆操作(数组左移,最左侧元素移动到最右侧)、交换 $ ak ai $ 即可。
完整代码
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
void out(int a[],int n)
{
for(int i=0;i<n;i++)
{
if(i!=n-1)printf("%d,",a[i]);
else printf("%d\n",a[i]);
}
}
void swap(int *a,int *b)
{
int t=*a;
*a=*b;
*b=t;
}
void move_left(int *a,int l,int r)
{
if(l>=r) return;
int temp=a[r];
for(int i=r;i>=l;i--)
{
a[i]=a[i-1];
}
a[l]=temp;
}
void move_right(int *a,int l,int r)
{
if(l>=r) return;
int temp=a[l];
for(int i=l;i<=r;i++)
{
a[i]=a[i+1];
}
a[r]=temp;
}
void solve(int a[],int k,int m)
{
if(k==m) out(a,m+1);
for(int i=k;i<=m;i++)
{
swap(&a[k],&a[i]);
move_left(a,k+1,i);
solve(a,k+1,m);
move_right(a,k+1,i);
swap(&a[k],&a[i]);
}
}
int main()
{
int n;
scanf("%d", &n);
int a[20];
for(int i=0;i<n;i++)
{
scanf("%d", &a[i]);
}
solve(a,0,n-1);
return 0;
}
Excel 演示
我们借助 VBA 可以让这个过程更加明显的展现在我们面前。
Excel 页面
VBA代码如下(没有任何可读性,内容和上述代码一致)
Private Declare PtrSafe Sub Sleep Lib "kernel32" (ByVal dwMilliseconds As Long)
Sub swap(a As Integer, b As Integer)
Dim t As Integer
t = Cells(4, a)
Cells(4, a) = Cells(4, b)
Cells(4, b) = t
End Sub
Sub move_left(l As Integer, r As Integer)
Dim i As Integer
If l < r Then
Cells(2, 3) = "左移开始"
Sleep Cells(2, 5)
For i = 1 To Cells(2, 1) Step 1
Cells(5, i) = Cells(4, i)
Next i
Sleep Cells(2, 5)
Dim t As Integer
t = Cells(4, r)
For i = r To l Step -1
Cells(4, i) = Cells(4, i - 1)
Next i
Cells(4, l) = t
Cells(2, 3) = "左移结束"
Sleep Cells(2, 5)
Cells(4, l) = t
Cells(2, 3) = " "
End If
End Sub
Sub move_right(l As Integer, r As Integer)
If l < r Then
Cells(2, 3) = "复原开始"
Sleep Cells(2, 5)
Dim t As Integer
Sleep Cells(2, 5)
t = Cells(4, l)
Sleep Cells(2, 5)
Dim i As Integer
For i = l To r Step 1
Cells(4, i) = Cells(4, i + 1)
Next i
Sleep Cells(2, 5)
Cells(4, r) = t
Cells(2, 3) = "复原结束"
Sleep Cells(2, 5)
For i = 1 To Cells(2, 1) Step 1
Cells(5, i) = " "
Next i
Cells(2, 3) = " "
End If
End Sub
Sub solve(k As Integer, m As Integer)
If (k = m) Then
Cells(2, 3) = "找到一个全排列!"
Dim cnt As Integer
cnt = Cells(6, 2)
Dim str, f As String
f = ","
Dim n, i As Integer
n = Cells(2, 1)
For i = 1 To n Step 1
If (i = n) Then
str = str & Cells(4, i)
Else
str = str & Cells(4, i) & f
End If
Next i
Cells(7 + cnt, 1) = str
Cells(6, 2) = cnt + 1
Cells(2, 3) = " "
End If
For i = k To m Step 1
Call swap(k, i)
Sleep Cells(2, 5)
Call move_left(k + 1, i)
Call solve(k + 1, m)
Call move_right(k + 1, i)
Call swap(k, i)
Next i
End Sub
Sub start()
Dim n As Integer
n = Cells(2, 1)
Call solve(1, n)
End Sub
总结
对于这个问题我们使用了两种方式求解,第一种是记忆化搜索,通过标记变量 f 及 ans 数组进行辅助求解;第二种是使用一个数组,在数组内不断交换元素进行求解。
两种解题思路各有利弊,第一种思维更简单,但需要额外开辟空间进行辅助。第二种则是通过重复利用a数组,避免了额外开辟空间。